Precyzyjne obliczanie powierzchni jest kluczowym elementem planowania budowlanego, projektowania wnętrz czy prac remontowych. Szczególnie istotne staje się to w przypadku nietypowych kształtów, takich jak trójkąty. W tym artykule przedstawimy różne metody obliczania pola trójkąta oraz innych figur często spotykanych w budownictwie, wraz z praktycznymi przykładami i gotowymi wzorami.
Spis treści
- Jak obliczyć metry kwadratowe w trójkącie za pomocą kalkulatora?
- Jak obliczyć pole trójkąta znając tylko długości boków?
- Jak obliczyć pole trójkąta znając dwa boki i kąt między nimi?
- Jak obliczyć pole trójkąta prostokątnego i równobocznego?
- Jak obliczyć objętość prostopadłościanu? – kalkulator i wzór
- Przeliczanie masy stali: z ton na kilogramy na metr (kg/m)
- Praktyczne przykłady obliczeń w budownictwie
- Podsumowanie: znaczenie precyzyjnych obliczeń w budownictwie
- Źródła
Jak obliczyć metry kwadratowe w trójkącie za pomocą kalkulatora?
Obliczanie pola powierzchni trójkąta może wydawać się skomplikowane, jednak z odpowiednimi narzędziami staje się proste. Istnieje kilka metod obliczania pola trójkąta, w zależności od tego, jakie dane posiadamy.
Przykładowy kalkulator do obliczania pola trójkąta
Podstawowy wzór na pole trójkąta
Najprostszy i najczęściej używany wzór na pole trójkąta wymaga znajomości długości podstawy i wysokości:
P = (a × h) ÷ 2
gdzie:
P – pole powierzchni trójkąta
a – długość podstawy trójkąta
h – wysokość trójkąta (prostopadła do podstawy)
Aby skorzystać z kalkulatora pola trójkąta, wystarczy wykonać kilka prostych kroków:
- Zmierz długość podstawy trójkąta (a)
- Zmierz wysokość trójkąta (h) – odległość od podstawy do przeciwległego wierzchołka
- Wprowadź obie wartości do kalkulatora
- Otrzymasz wynik w metrach kwadratowych (m²)
Przykład: Jeśli podstawa trójkąta ma długość 4 m, a wysokość wynosi 3 m, to pole powierzchni wynosi: P = (4 × 3) ÷ 2 = 6 m².
Jak obliczyć pole trójkąta znając tylko długości boków?
W praktyce budowlanej często nie mamy możliwości bezpośredniego zmierzenia wysokości trójkąta. W takich przypadkach przydaje się wzór Herona, który pozwala obliczyć pole trójkąta znając tylko długości jego trzech boków.
Wzór Herona
Wzór Herona to matematyczna formuła opracowana przez Herona z Aleksandrii około 60 r. n.e., która umożliwia obliczenie pola trójkąta na podstawie długości jego boków:
P = √[p(p-a)(p-b)(p-c)]
gdzie:
P – pole powierzchni trójkąta
a, b, c – długości boków trójkąta
p – połowa obwodu trójkąta: p = (a + b + c) ÷ 2
Aby obliczyć pole trójkąta za pomocą wzoru Herona, wykonaj następujące kroki:
- Zmierz dokładnie wszystkie trzy boki trójkąta (a, b, c)
- Oblicz połowę obwodu: p = (a + b + c) ÷ 2
- Podstaw wartości do wzoru: P = √[p(p-a)(p-b)(p-c)]
- Oblicz wartość pod pierwiastkiem
- Wyciągnij pierwiastek kwadratowy z otrzymanej wartości
Przykład: Dla trójkąta o bokach a = 5 m, b = 6 m, c = 7 m:
1. p = (5 + 6 + 7) ÷ 2 = 9 m
2. P = √[9 × (9-5) × (9-6) × (9-7)]
3. P = √[9 × 4 × 3 × 2]
4. P = √216 ≈ 14,7 m²
Jak obliczyć pole trójkąta znając dwa boki i kąt między nimi?
W niektórych sytuacjach znamy dwa boki trójkąta oraz kąt zawarty między nimi. W takim przypadku możemy skorzystać z wzoru trygonometrycznego.
P = (a × b × sin γ) ÷ 2
gdzie:
P – pole powierzchni trójkąta
a, b – długości dwóch boków trójkąta
γ (gamma) – kąt między bokami a i b (w stopniach)
sin γ – sinus kąta gamma
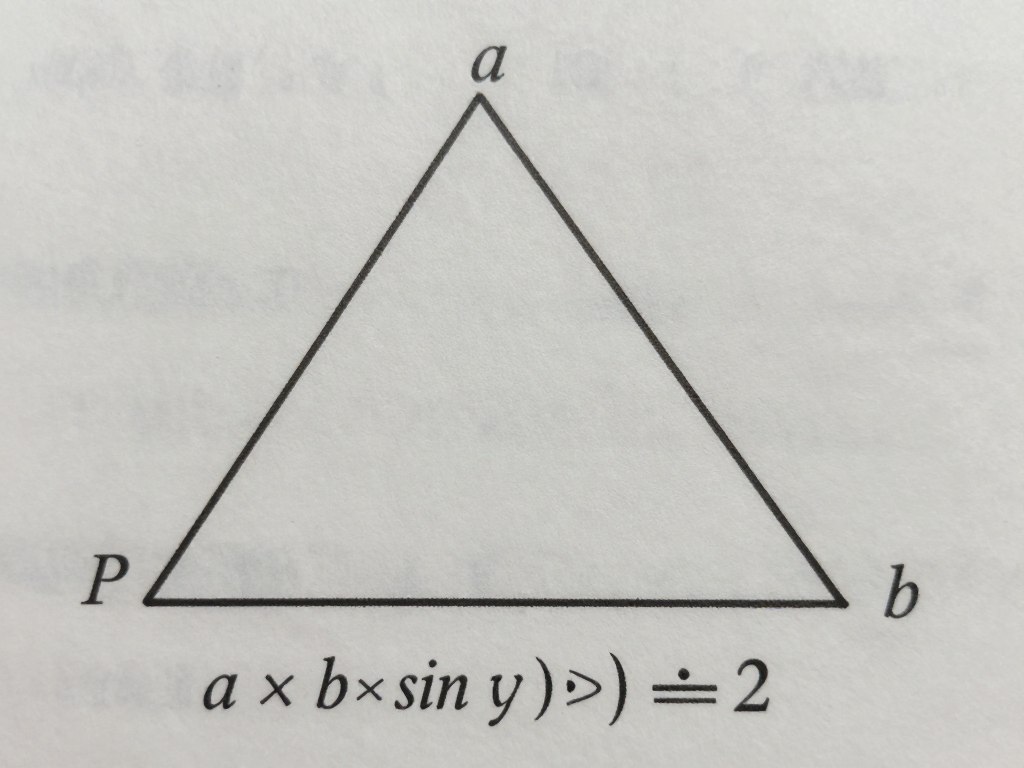
Przykład: Jeśli dwa boki trójkąta mają długości a = 4 m i b = 5 m, a kąt między nimi wynosi γ = 30°, to pole powierzchni wynosi:
P = (4 × 5 × sin 30°) ÷ 2
P = (4 × 5 × 0,5) ÷ 2 = 5 m²
Ta metoda jest szczególnie przydatna w przypadku pomiarów terenowych, gdzie łatwiej jest zmierzyć kąty niż wysokości.
Jak obliczyć pole trójkąta prostokątnego i równobocznego?
Niektóre rodzaje trójkątów mają specjalne właściwości, które upraszczają obliczanie ich pola. Przyjrzyjmy się dwóm najpopularniejszym przypadkom.
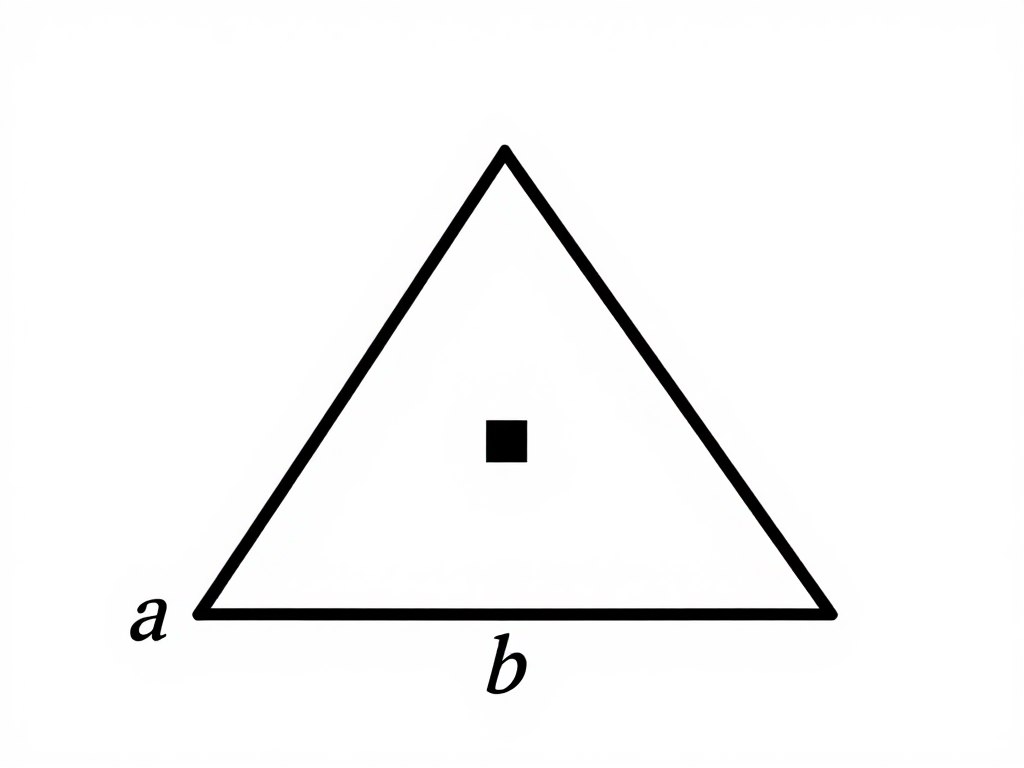
Trójkąt prostokątny
W przypadku trójkąta prostokątnego, pole można obliczyć mnożąc długości przyprostokątnych i dzieląc wynik przez 2:
P = (a × b) ÷ 2
gdzie a i b to długości przyprostokątnych (boków tworzących kąt prosty)
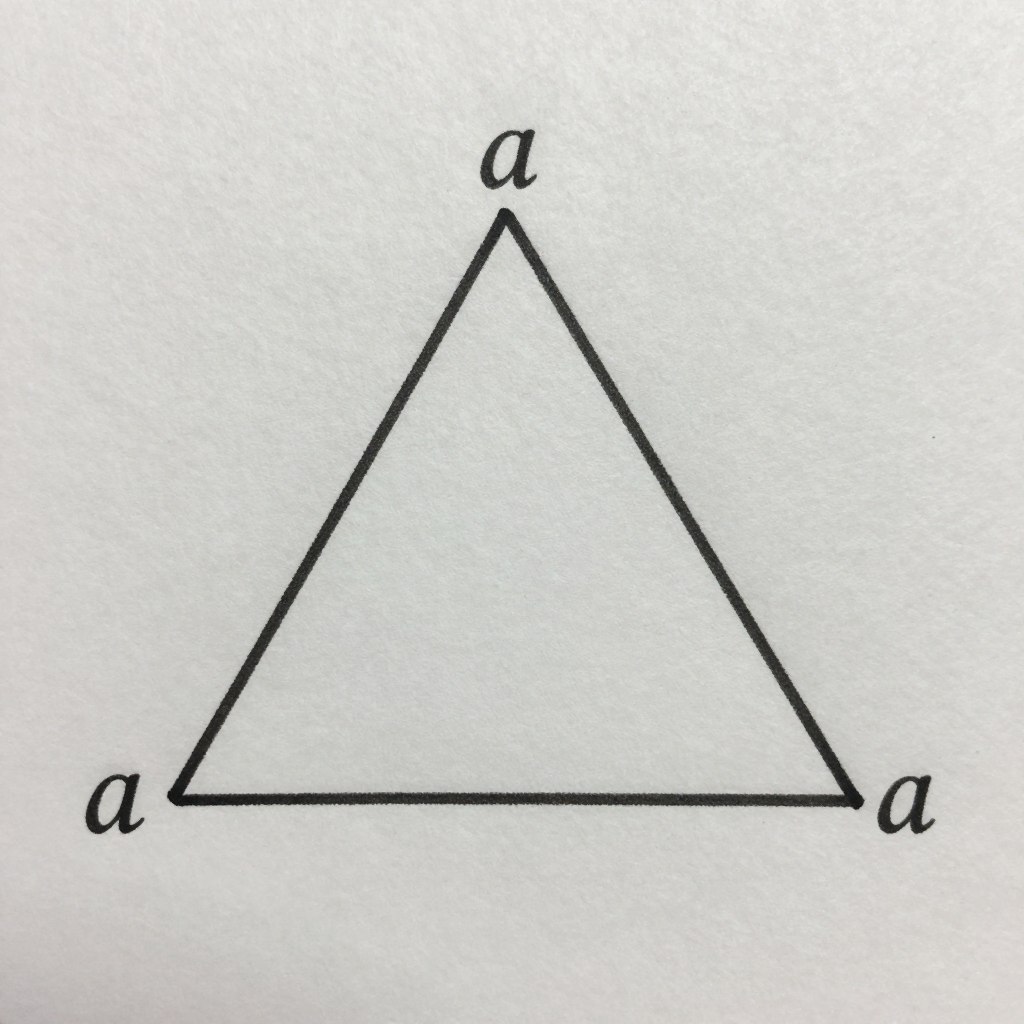
Trójkąt równoboczny
Dla trójkąta równobocznego, w którym wszystkie boki mają taką samą długość, pole można obliczyć za pomocą wzoru:
P = (a² × √3) ÷ 4
gdzie a to długość boku trójkąta równobocznego
Przykład: Dla trójkąta równobocznego o boku a = 6 m:
P = (6² × √3) ÷ 4 = (36 × 1,732) ÷ 4 ≈ 15,59 m²
Jak obliczyć objętość prostopadłościanu? – kalkulator i wzór
W budownictwie często potrzebujemy obliczyć nie tylko powierzchnię, ale również objętość. Prostopadłościan (w tym sześcian) to jedna z podstawowych brył przestrzennych, której objętość łatwo obliczyć.
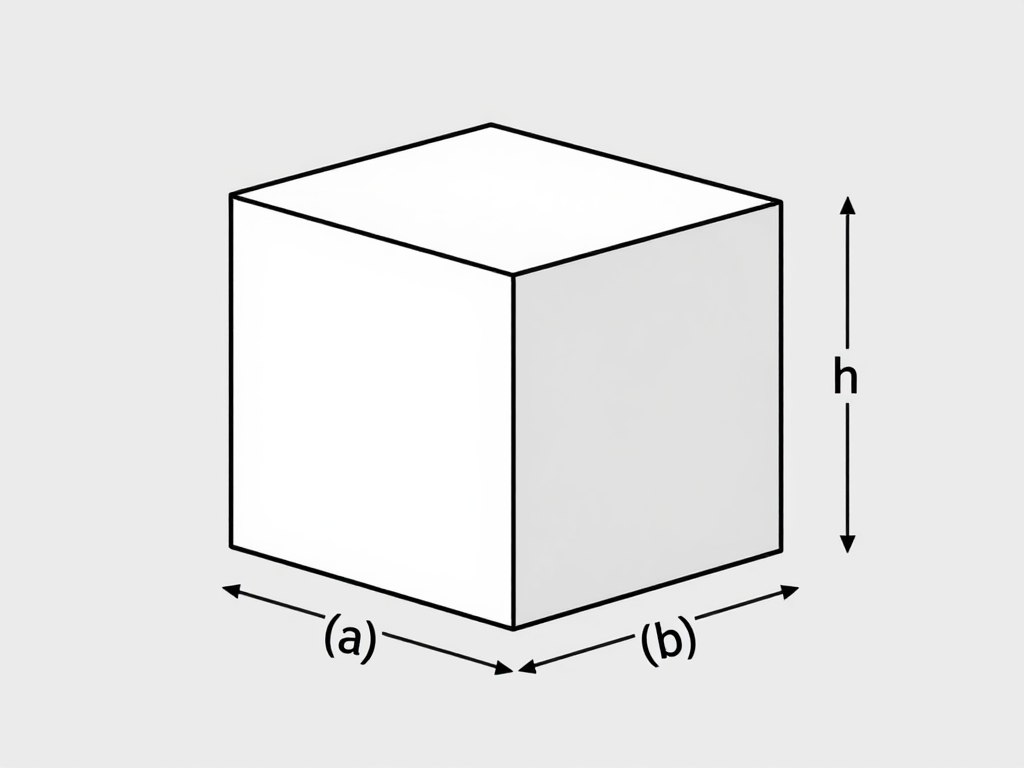
Wzór na objętość prostopadłościanu
Objętość prostopadłościanu obliczamy mnożąc jego długość, szerokość i wysokość:
V = a × b × h
gdzie:
V – objętość prostopadłościanu
a – długość prostopadłościanu
b – szerokość prostopadłościanu
h – wysokość prostopadłościanu
Przykład: Jeśli prostopadłościan ma wymiary a = 3 m, b = 4 m i h = 2,5 m, to jego objętość wynosi:
V = 3 × 4 × 2,5 = 30 m³
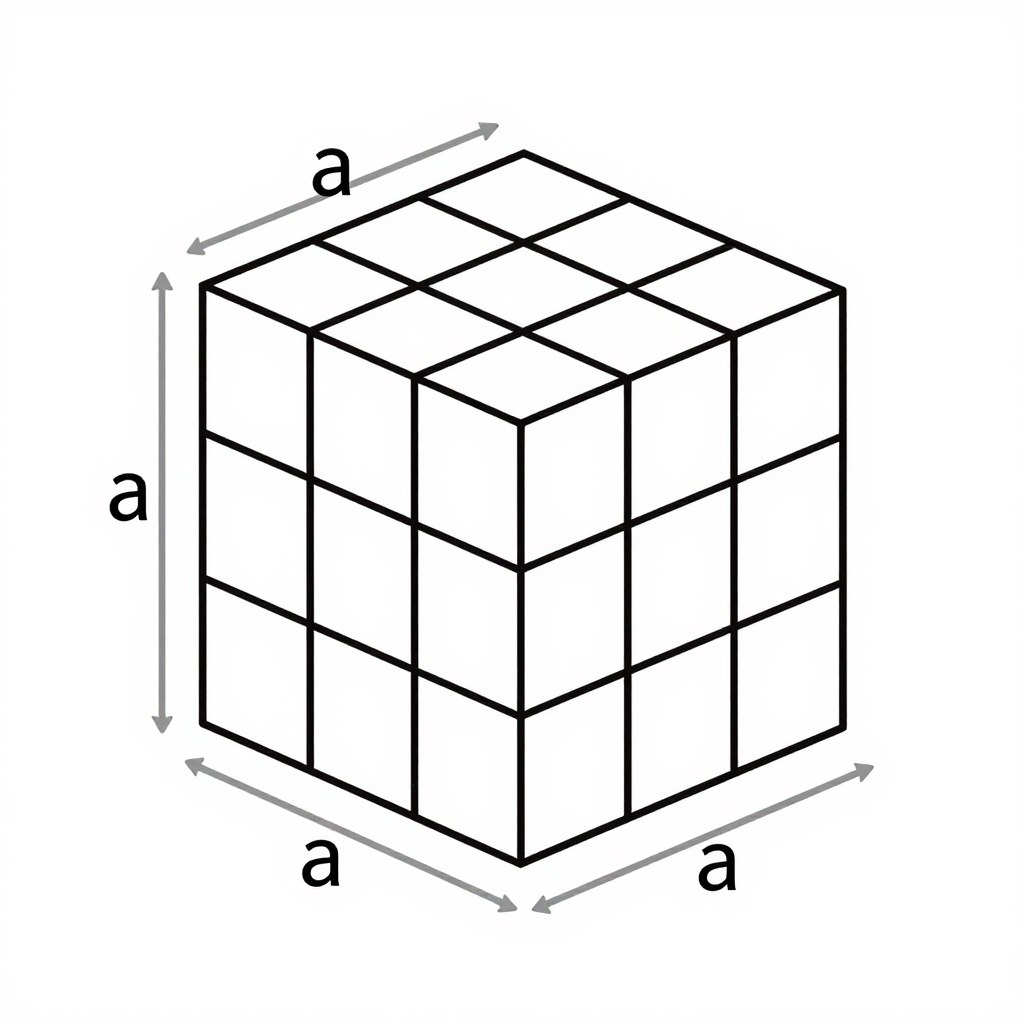
W przypadku sześcianu, gdzie wszystkie krawędzie mają taką samą długość, wzór upraszcza się do:
V = a³
gdzie a to długość krawędzi sześcianu
Przeliczanie masy stali: z ton na kilogramy na metr (kg/m)
W projektach budowlanych często potrzebujemy obliczyć masę elementów stalowych, takich jak pręty zbrojeniowe, profile czy blachy. Poniżej przedstawiamy, jak to zrobić.

Obliczanie masy stali na podstawie gęstości
Gęstość stali konstrukcyjnej wynosi około 7850 kg/m³. Aby obliczyć masę elementu stalowego, należy pomnożyć jego objętość przez gęstość:
m = V × ρ
gdzie:
m – masa elementu stalowego [kg]
V – objętość elementu [m³]
ρ (ro) – gęstość stali (7850 kg/m³)
Masa pręta stalowego na metr
Dla pręta o przekroju kołowym, masę na metr bieżący obliczamy według wzoru:
m = π × (d/2)² × ρ
gdzie:
m – masa pręta na metr [kg/m]
d – średnica pręta [m]
ρ – gęstość stali (7850 kg/m³)
Przykład: Dla pręta o średnicy d = 12 mm = 0,012 m:
m = 3,14159 × (0,012/2)² × 7850 = 0,89 kg/m

Masa profili stalowych
Dla profili stalowych (dwuteowniki, ceowniki, kątowniki) producenci zwykle podają masę na metr bieżący w katalogach. Można też ją obliczyć, mnożąc pole przekroju profilu przez gęstość stali:
m = A × ρ
gdzie:
m – masa profilu na metr [kg/m]
A – pole przekroju profilu [m²]
ρ – gęstość stali (7850 kg/m³)

Praktyczne przykłady obliczeń w budownictwie
Poniżej przedstawiamy kilka praktycznych przykładów, które pokazują, jak wykorzystać omówione wzory w rzeczywistych sytuacjach budowlanych.
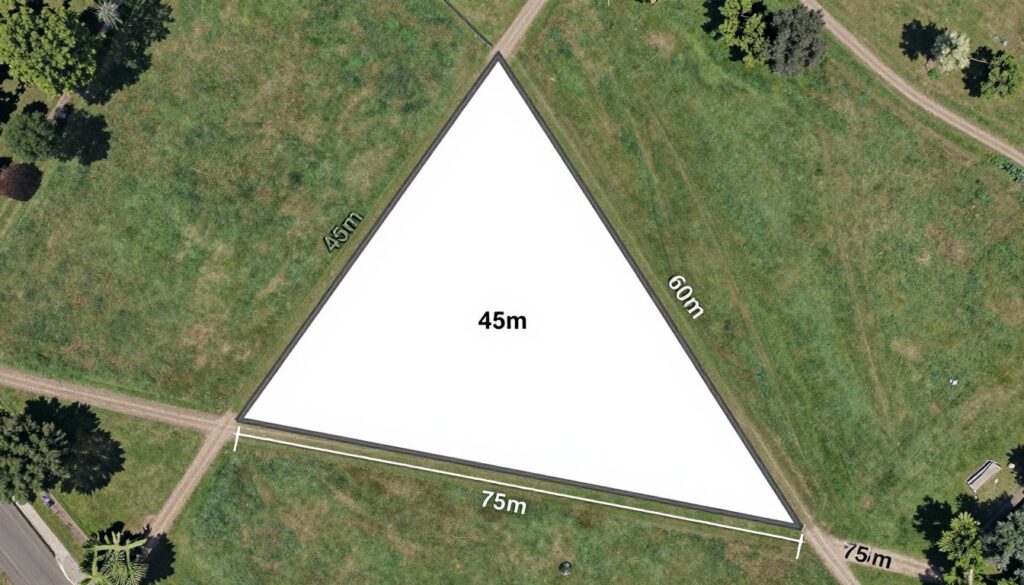
Przykład 1: Obliczanie powierzchni działki
Działka ma kształt trójkąta o bokach 45 m, 60 m i 75 m. Obliczmy jej powierzchnię za pomocą wzoru Herona:
p = (45 + 60 + 75) ÷ 2 = 90 m
P = √[90 × (90-45) × (90-60) × (90-75)]
P = √[90 × 45 × 30 × 15]
P = √1822500 ≈ 1350 m²
Przykład 2: Obliczanie objętości fundamentu
Fundament ma kształt prostopadłościanu o wymiarach 8 m × 12 m × 0,8 m. Obliczmy jego objętość:
V = 8 × 12 × 0,8 = 76,8 m³
Znając objętość, możemy obliczyć ilość potrzebnego betonu oraz jego masę (gęstość betonu wynosi około 2400 kg/m³):
m = 76,8 × 2400 = 184320 kg = 184,32 tony
Przykład 3: Obliczanie masy zbrojenia
Do zbrojenia fundamentu potrzebujemy 120 prętów o średnicy 12 mm i długości 7,5 m każdy. Obliczmy całkowitą masę zbrojenia:
Masa jednego pręta na metr: 0,89 kg/m
Masa jednego pręta: 0,89 × 7,5 = 6,675 kg
Całkowita masa: 6,675 × 120 = 801 kg
Podsumowanie: znaczenie precyzyjnych obliczeń w budownictwie
Precyzyjne obliczenia matematyczne są fundamentem każdego udanego projektu budowlanego. Pozwalają na dokładne zaplanowanie ilości potrzebnych materiałów, co przekłada się na optymalizację kosztów i minimalizację odpadów. Znajomość podstawowych wzorów na obliczanie pola trójkąta, objętości prostopadłościanu czy masy elementów stalowych jest niezbędna zarówno dla profesjonalistów, jak i dla osób realizujących własne projekty budowlane.
Warto pamiętać, że w przypadku bardziej skomplikowanych obliczeń zawsze można skorzystać z dostępnych online kalkulatorów, które znacznie ułatwiają pracę. Jednak zrozumienie podstawowych zasad matematycznych pozwala na weryfikację otrzymanych wyników i uniknięcie potencjalnych błędów.

Źródła
[1] Wzory matematyczne – https://www.matematyka.pl/wzory
[2] Kalkulator pola trójkąta – https://www.omnicalculator.com/pl/matematyka/pole-trojkata
[3] Kalkulator pola trójkąta o danych bokach – https://www.omnicalculator.com/pl/matematyka/pole-trojkata-o-danych-bokach
[4] Kalkulator trójkąta prostokątnego – https://www.omnicalculator.com/pl/matematyka/trojkat-prostokatny
[5] Normy budowlane: Obliczanie objętości i masy elementów budowlanych – https://www.pkn.pl
[6] Katalog wyrobów stalowych – https://www.stal-hurt.com/katalog
[7] Poradnik inżyniera: Matematyka w budownictwie – https://www.inzynierbudownictwa.pl

Redaktor Naczelny | Ekspert ds. Energetyki Rozproszonej
Inżynier z zamiłowania, analityk z wyboru. Adam od ponad dekady związany jest z polskim sektorem energetycznym. Doświadczenie zdobywał zarówno przy projektowaniu farm fotowoltaicznych, jak i w działach analiz banków finansujących zielone inwestycje.
W VexEnergy.pl dba o to, by trudny język inżynierski przekładać na zrozumiałe dla każdego „Kowalskiego” porady. Prywatnie pasjonat elektromobilności i tester domowych systemów magazynowania energii. Jego cel? Sprawić, by Polska była energetycznie niezależna – dom po domu.